关于FFT的原理可以参照之前的一篇课程报告:[Report] 基于快速傅里叶变换的大数乘法原理分析
以及_Orchidany的博客:FFT·快速傅里叶变换
本文主要参照该博客实现方式,通过C++实现FFT,对博客中部分内容作了补充说明,包含递归法和迭代法。
首先有复数运算类(此处用不到乘法就不写了):
struct Complex {
double x, y;
Complex (double xx = 0, double yy = 0): x(xx), y (yy) { }
inline Complex operator+(const Complex &c2) const {
return Complex(x + c2.x, y + c2.y);
}
inline Complex operator-(const Complex &c2) const {
return Complex(x - c2.x, y - c2.y);
}
inline Complex operator*(const Complex &c2) const {
return Complex(x * c2.x - y * c2.y, x * c2.y + y * c2.x);
}
};我们总是设flag==0时为FFT,flag==1时为IFFT。
根据FFT原理,容易写出如下递归代码:
void fft(Complex *c, int len, int flag)
{
if (len == 1) return;
int mid = len >> 1;
Complex A0[mid], A1[mid];
for (int i = 0; i <= len; i += 2)
A[i >> 1] = A[i], A[i >> 1] = A[i + 1]; //将系数按奇偶分开
fft(A0, mid, flag);
fft(A1, mid, flag);
Complex unit(cos(2 * PI / len), sin(2 * PI / len)); //单位原根
Complex w(1, 0);
for (int i = 0; i < mid; i++, w = w * unit) {
Complex t = w * A1[i]; //蝴蝶变换
c[i] = A0[i] + t;
c[i + mid] = A0[i] - t;
}
} //注意若flag==-1,应将最终结果除以区间长度由于递归版本FFT常数很大,下面考虑将代码改进为迭代版本,我们观察递归过程中系数位置的变化规律,同时注意到其实只需要将系数交换到最终(最下方)的位置,然后倒着合并问题即可:
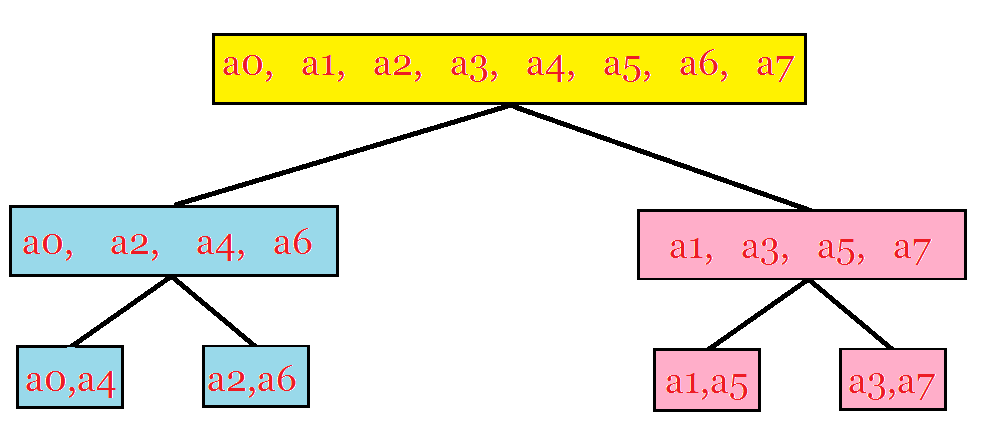
有如下规律(原博客第5个数字有误):
原来的序号 0 1 2 3 4 5 6 7
现在的序号 0 4 2 6 1 5 3 7
原来的二进制表示 000 001 010 011 100 101 110 111
现在的二进制表示 000 100 010 110 001 101 011 111
也就是最终位置的二进制串正好是起始位置的二进制串的逆序(不是取反)。
我们可以考虑使用递推来计算逆序对应的数字。
设有数字x,逆序rev(x)。
则x左移1位时,rev(x)右移了1位,也就是rev(x) >> 1。
而当x增加1时,此时x可以看作之前某个数y左移1位y << 1后最高位的数字发生变化,并且实际上和x+1最低位一样,所以取出最低位数字放到最右边,然后或上将x >> 1逆序右移1一位就是新的逆序。
因此得到如下的递推程序;
for (int i = 1; i <= lim; i++)
rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (log2_lim - 1));最后我们只需要通过三重for循环控制进行迭代即可,最外层循环实际上模拟递归深度,同时也控制子问题的左右两半,第二层模拟的是不同的子问题,最内层模拟的是子问题下待合并的数据:
void FFT(Complex *c, int flag)
{
for (int i = 0; i < lim; i++)
if (i < rev[i]) // 防止重复交换
swap(c[i], c[rev[i]]);
for (int j = 1; j < lim; j <<= 1) { // log2_lim-j 递归层数
Complex w(cos(PI / j), flag * sin(PI / j)); // 本来区间长度len时应为exp(flag*2*PI/len),但待合并区间长度正好为2j
int j2 = j << 1;
for (int k = 0; k < lim; k += j2) { // k 每层待合并的子问题
Complex t(1, 0);
for (int l = 0; l < j; l++, t = t * w) { // l 每个子问题下的数据偏移量
int kl = k + l;
Complex Nx = c[kl], Ny = t * c[kl + j]; // 蝴蝶变换,Nx为偶数项,Ny为奇数项
c[kl] = Nx + Ny; // 左半部分合并
c[kl + j] = Nx - Ny; // 右半部分合并
}
}
}
if (flag == -1) // 处理IFFT变换系数
for (int i = 0; i <= lim; i++)
c[i].x = c[i].x / lim; // 虚部趋于0不作处理
}注意交换时只能交换一次,这就是迭代版本的FFT。
例题:
P1919 【模板】A*B Problem 升级版(FFT 快速傅里叶变换)
P3803 【模板】多项式乘法(FFT)
贴个AC图[/斜眼笑]