[Note] Quantum Error Correction: Error Types and Parity Check

I recently try to do some work on quantum computing, and thus focus on reading some papers and blogs.

Since I came from a math background, I may poccess a view that is different from those from physics and computer science. I will collect some notes here for what I've read for better understanding. Note that this is just my own notes, and it may not be suitable for others.

This note is collected from
The stabilizer trilogy I — Stabilizer codes by Arthur Pesah

I learned classical error correction during my undergrad, and I totally understand it's never been a simple thing. Now introducing quantum qubits, which can be considered as continuized classical bits, leads things to a mess. Let's start from the most rudimentary thoughs, repetition code.

A qubit can be described as

\ket{\psi}=a\ket{0}+b\ket{1}=(a,b)^T,a,b\in \mathbb{C},|a|^2+|b|^2=1.

We know there three kinds of Pauli operators X,Y,Z, with

\begin{aligned}
X&=\begin{pmatrix} 0 & 1 \\
1 & 0 \end{pmatrix},\\
Y &= \begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix},\\
Z &= \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}.
\end{aligned}

They satisfy commutation relation

\begin{aligned}
[X,Y]&=iZ,\\
[Y,Z]&=iX,\\
[Z,X]&=iY,
\end{aligned}

and anti-commutation

\{X,Y\}=\{X,Z\}=\{Y,Z\}=0.

Generally, there are two types of quantum error. X error flip the bits as

X\ket{\psi}=a\ket{1}+b\ket{0},

whereas Z error flip the phase as

Z\ket{\psi}=a\ket{0}-b\ket{1}.

How about Y error

Y\ket{\psi}=-ib\ket{0}+ia\ket{1}.

It's equivalent to

Y\ket{\psi}=iXZ\ket{\psi}.

Since any Hermitian matrices can be decomposed using Pauli matrix basis along with I, any qubit error can be described by X and Z error.

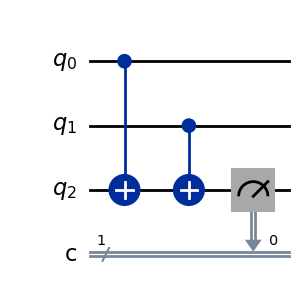
Consider finding the X error for two qubits, we can do similar things by checking the parity as we do in classical error check (e.g. in TCP protocol).

However, we cannot measure a qubit without collapsing it, so it's impossible to do direct measurement.

Using two CNOT gates, where we input a \ket{0} and two to-be-measured qubits as control end. We can measure the output of CNOT gate to get the parity operator Z_0Z_1. We can easily see that

\begin{aligned}
Z_0Z_1\ket{00}&=\ket{00},\\
Z_0Z_1\ket{11}&=\ket{11},
\end{aligned}

but

\begin{aligned}
Z_0Z_1\ket{01}&=-\ket{01},\\
Z_0Z_1\ket{10}&=-\ket{10}.
\end{aligned}

This is an example of parity check by two CNOT gates.

Apply all possible Z_iZ_j helps to corrects X errors. For example, if we have three qubits as repetition code (one logical qubit)

\ket{\psi}=a\ket{000}+b\ket{111},

and an X error happens to the first qubit

X_1\ket{\psi}=a\ket{100}+b\ket{011}.

By doing parity check for qubit 1 and qubit 2, qubit 1 and qubit 3, we have

\begin{aligned}
Z_1Z_2X_1\ket{\psi}&=-a\ket{100}-b\ket{011}=-X_1\ket{\psi},\\
Z_1Z_3X_1\ket{\psi}&=-a\ket{100}-b\ket{011}=-X_1\ket{\psi}.
\end{aligned}

But for qubit 2 and qubit 3, we have

Z_1Z_3X_1\ket{\psi}=a\ket{100}+b\ket{011}=X_1\ket{\psi}.

Therefore, the error must happend in qubit 1 (assume there only one error).

This is very similar to classical repetition code. However, the different thing is that it cannot detect all errors, such as Z error. This is because X is anti-commutative with Z. But Z is commutative with Z, and we cannot detect Z error using this method.

In conclusion,

• All error-free states are eigenstates of Z_iZ_j with eigenvalue +1.
• Error operator Z_k are anti-commutative with some Z_iZ_j, i.e. error states are eigenstates of some Z_iZ_j with eigenvalue -1.

This concept can be further to be stablizer group and its corresponding codes. Using group theory, we can draw a clear picture of logical qubits and logical gates under much more complex codes.