这学期选了数据结构课,讲到了利用栈进行表达式求值,在此做简单的笔记并进行了简单Python实现。
表达式树与表达式类型
我们日常书写的表达式又叫中缀表达式,例如:9+(6-3)*2+7,特点是运算符都位于运算数之间,同时为了手写方便在一定的运算符优先级下我们通过括号来规定次序。
这在计算机中处理是不方便的,计算机中更常用的是后缀表达式,你应该也猜到了,其实还有前缀表达式。
所谓前缀、中缀、后缀表达式,一方面可以看运算符与运算数的位置关系,同时我们可以通过生成语法树来得到,三种表达式分别对应于树的前序、中序、后序遍历。所谓语法树,就是讲运算数放在叶子节点,运算符(不包含括号)放在父节点的树,由于我们的运算符多半是二目运算符,因此语法树通常也是二叉树。
例如上面的表达式对应语法树:
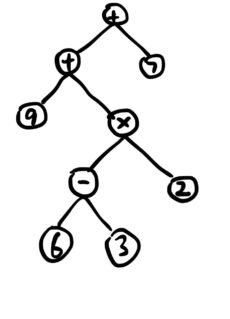
对应遍历或表达式
前序遍历:+ + 9 - 6 3 2 7
中序遍历:9 + 6 - 3 2 + 7
后序遍历:9 6 3 - 2 * + 7 +
后缀表达式的生成
但是事实上为了从日常书写的表达式生成后缀表达式我们是不需要生成整个语法树的,利用栈即可。
具体原理大概是:
- 在没有括号时,如果运算符优先级在某一区域是从左往右不严格递增的,那么其实我们最终需要从右向左计算,此时只需要先将运算数排好,再将运算符挨个排到后面即可。
- 在没有括号,如果运算符优先级出现了小于等于上一个的情况,此时说明前面的需要先计算,于是我们先生成前面的后缀表达式,再继续处理后面的。
- 如果有括号,只需要确保括号结束后有所有运算符,那么括号内也是单独计算的。
我们逐个遍历原表达式,并进行如下操作:
- 如果遇到运算数,则追加到后缀表达式。
- 如果遇到运算符,则我们将其放入到栈中,遇到左括号时我们也将其放入栈中。
- 如果遇到一个右括号,则将栈元素弹出,将弹出的操作符输出直到遇到左括号为止。再将左括号直接弹出。
- 如果遇到的是其他运算符(包含左括号),则从栈顶开始,不断比较栈顶运算符和当前运算符的优先级,并且弹出到后缀表达式,直到找到第一个优先级(括号优先级始终大于任何运算符)低于当前运算符的运算符,或者栈为空,或者遇到左括号则停止,在栈中插入当前运算符。
- 读入到原表达式末尾,则按入栈顺序完全弹出到后缀表达式上。
最后我们得到后缀表达式,接下来处理该表达式即可。
后缀表达式求值
后缀表达式求值是简单的,遵循遇到数字则入栈,遇到操作符则出栈两个数字,按照操作符进行计算的原则即可,对于没有交换性的运算符,需要特别注意运算顺序,因为元素出栈顺序是从右向左的。
以下是代码实现:
from decimal import DivisionByZero
class SqStack():
'''
顺序存储的栈
'''
def __init__(self):
self.data = []
self.n = 0
def push(self, x):
if self.n == len(self.data):
self.data.append(x)
self.data[self.n] = x
self.n += 1
def not_empty(self) -> bool:
return self.n >= 1
def pop(self):
assert self.not_empty()
self.n -= 1
def top(self):
assert self.not_empty()
return self.data[self.n - 1]
def calc(expr) -> float:
is_numexpr = lambda ch: ch.isdigit() or ch == '.' # 判断是否为数字的一部分
is_opt = lambda ch: ch == '+' or ch == '-' or ch == '*' or ch == '/' or ch == '(' # 判断是否为需要入栈的操作符
opt_priority = {'+':0, '-':0, '*':1, '/':1, '(':2} # 运算符优先级,数字越大优先级越大
post_expr = [] # 存储后缀表达式
stk = SqStack() # 辅助栈
head_flag = True # 处理负数
end = len(expr)
i = 0
while i < end:
if expr[i] == ')':
head_flag = False
if (stk.not_empty()):
opt = stk.top(); stk.pop()
while opt != '(': # 遇到右括号不断弹出直到左括号
post_expr.append(opt)
if (stk.not_empty()):
opt = stk.top(); stk.pop()
elif is_numexpr(expr[i]) or (expr[i] == '-' and head_flag): # 遇到数字则找到整个数字后进行转换
head_flag = False
j = i + 1
while j < len(expr) and is_numexpr(expr[j]):
j += 1
post_expr.append(float(expr[i:j]))
i = j - 1
elif is_opt(expr[i]):
if expr[i] == '(': head_flag = True
else: head_flag = False
prior = opt_priority[expr[i]]
if stk.not_empty():
top_opt = stk.top()
while (top_opt != '(' and prior <= opt_priority[top_opt]): # 寻找第一个优先级小于的运算符
stk.pop()
post_expr.append(top_opt)
if stk.not_empty():
top_opt = stk.top()
else: break
stk.push(expr[i])
i += 1
while (stk.not_empty()):
post_expr.append(stk.top())
stk.pop()
for item in post_expr:
if type(item) == str:
num_2 = stk.top(); stk.pop() # 按入栈顺序取两个操作数进行计算
num_1 = stk.top(); stk.pop()
if item == '+':
stk.push(num_1 + num_2)
elif item == '-':
stk.push(num_1 - num_2)
elif item == '*':
stk.push(num_1 * num_2)
elif item == '/':
if abs(num_2) < 1e-300:
raise DivisionByZero
else: stk.push(num_1 / num_2)
else:
stk.push(item)
ans = stk.top(); stk.pop()
return ans
expr = input('Input a expression to calculate:\n')
try:
print(calc(expr))
except DivisionByZero:
print('Divided by zero!')
except Exception:
print('Syntax error!')